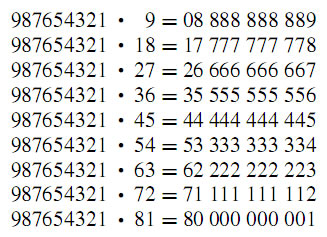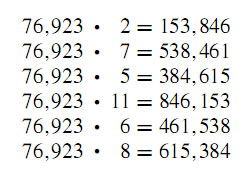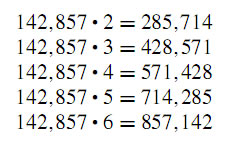Suprising Number Patterns III

Here are some more charmers of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Just look, enjoy, and spread these amazing properties to your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this. You might ask them why multiplying by 9 might give such unusual results. Once they see that 9 is one less than the base 10, they might get other ideas to develop multiplication patterns. A clue might be to have them consider multiplying by 11 (one greater than the base) to search for a pattern.

A similar process yields another interesting pattern. Might this give your students more impetus to search further?

Now the logical thing to inspect would be the pattern of these strange products.

How might you describe this pattern? Let students describe it in their own terms.

Panduan SEO dari Google

Google akhirnya merilis SEO starter guide atau panduan dasar SEO dalam 40 bahasa setelah sebelumnya hanya merilis dalam bahasa inggris.

link download dalam bahasa inggris
Search Engine Optimization Starter Guide
http://www.google.com/webmasters/docs/search-engine-optimization-starter-guide.pdf

link download dalam bahasa indonesia
Panduan Dasar SEO
http://www.google.co.id/intl/id/webmasters/docs/search-engine-optimization-starter-guide-id.pdf

Untuk yang gak mengerti bahasa inggris ataupun indonesia, silahkan melihat hlaman dibawah ini :
Google SEO Starter Guide
http://googlewebmastercentral.blogspot.com/2008/11/googles-seo-starter-guide.html

Kesimpulan.
Sayang sekali sepertinya format dalam bahasa indonesia ini hasil terjemahan kasar oleh Google Translator. Sehingga hasilnya kurang maksimal. Sampai-sampai lidah saya terlipat bacanya. hehehe. Anyway, saya bersyukur aja google udah SEO Starter Guide ini.

Suprising Number Patterns II

Here are some more charmers of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Just look, enjoy, and share these amazing properties with your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this.

In the following pattern chart, notice that the first and last digits of the products are the digits of the multiples of 9.

It is normal for students to want to find extensions of this surprising pattern. They might experiment by adding digits to the first multiplicand or by multiplying by other multiples of 9. In any case, experimentation ought to be encouraged.

Suprising Number Patterns I

There are times when the charm of mathematics lies in the surprising nature of its number system. There are not many words needed to demonstrate this charm. It is obvious from the patterns attained. Look, enjoy, and spread these amazing properties to your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this. Most important is that the students can get an appreciation for the beauty in these number patterns.

Notice (below) how various products of 76,923 yield numbers in the same order but with a different starting point. Here the first digit of the product goes to the end of the number to form the next product. Otherwise, the order of the digits is intact.

Notice (below) how various products of 76,923 yield different numbers from those above, yet again, in the same order but with a different starting point. Again, the first digit of the product goes to the end of the number to form the next product. Otherwise, the order of the digits is intact.

Another peculiar number is 142,857. When it is multiplied by the numbers 2 through 8, the results are astonishing. Consider the following products and describe the peculiarity.

You can see symmetries in the products but notice also that the same digits are used in the product as in the first factor. Furthermore, consider the order of the digits. With the exception of the starting point, they are in the same sequence.

Now look at the product, 142,857 • 7 = 999,999. Surprised ?

It gets even stranger with the product, 142,857 • 8 = 1,142,856. If we remove the millions digit and add it to the units digit, the original number is formed.

It would be wise to allow the students to discover the patterns themselves. You can present a starting point or a hint at how they ought to start and then let them make the discoveries themselves. This will give them a sense of “ownership” in the discoveries. These are just a few numbers that yield strange products.