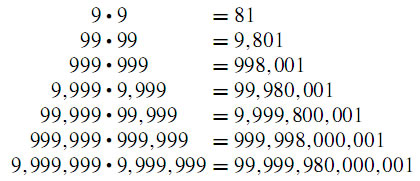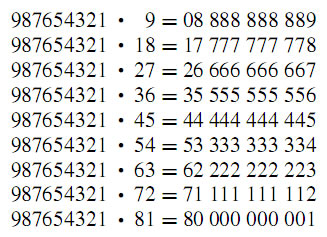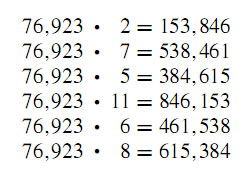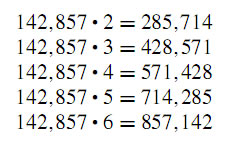Tukeran Link

Halo Semua bloggers akhirnya daku tergoda juga untuk melakukan tukeran link.

Bagi yang berniat silahkan komentari post ini untuk merequest backlink dengan syarat :

• anchor text ke situs ini blogupiel
• linknya http://blogupiel.blogspot.com

Daftar situs yang sudah request :

1. Dmegs Web Directory
   

The Fabulous Fibonacci Numbers

This post is to inspire teachers and students how beatifull Fibonacci numbers. There aren’t many themes in mathematics that permeate more branches of mathematics than the Fibonacci numbers. They come to us from one of the most important books in Western history. This book, Liber Abaci, written in 1202 by Leonardo of Pisa, more popularly known as Fibonacci (1180–1250), * or son of Bonacci, is the first European publication using the Hindu–Arabic numerals that are the basis for our base 10 number system. This alone would qualify it as a landmark book. However, it also contains a "harmless" problem about the regeneration of rabbits. It is the solution of that problem that produces the Fibonacci numbers.

You might have your students try to set up a chart and solve the problem independently before progressing further. It may be stated as follows:

How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair, which becomes productive from the second month on?

It is from this problem that the famous Fibonacci sequence emerged. If we assume that a pair of baby (B) rabbits matures in one month to become offspring-producing adults (A), then we can set up the following chart :

If we let fn be the nth term of the Fibonacci sequence, then :

That is, each term after the first two terms is the sum of the two preceding terms.

Your students may (rightly) ask at this point, What makes this sequence of numbers so spectacular? For one thing, there is a direct relationship between (believe it or not) it and the Golden Section! Consider successive quotients of the Fibonacci numbers:

Furthermore, you can refer students to notice that successive powers of * present us with the Fibonacci numbers.

If, by now, the students didn’t see the connection, highlight the coefficients and the constants. This is quite incredible; two completely (seemingly) unrelated things suddenly in close relationship to one another. That’s what makes mathematics so wonderful!

---

* Fibonacci was not a clergyman, as might be expected of early scientists; rather, he was a merchant who traveled extensively throughout the Islamic world and took advantage of reading all he could of the Arabic mathematical writings. He was the first to introduce the Hindu–Arabic numerals to the Christian world in his Liber abaci (1202 and revised in 1228), which first circulated widely in manuscript form and was first published in 1857 as Scritti di Leonardo Pisano (Rome: B. Buoncompagni). The book is a collection of business mathematics, including linear and quadratic equations, square roots and cube roots, and other new topics, seen from the European viewpoint. He begins the book with the comment: “These are the nine figures of the Indians 9 8 7 6 5 4 3 2 1. With these nine figures, and with the symbol 0, which in Arabic is called zephirum, any number can be written, as will be demonstrated below”. From here on, he introduces the decimal position system for the first time in Europe. (Note: The word “zephirum” evolved from the Arabic word as-sifr, which comes from the Sanskrit word, used in India as early as the fifth century,“sunya,” referring to empty.)

Suprising Number Patterns IV

Here are some more curiosities of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Yet in this case, you will notice that much is dependent on the number 1,001, which is the product of 7, 11, and 13. Furthermore, when your students multiply 1,001 by a three-digit number the result is nicely symmetric. For example, 987 • 1,001 = 987,987. Let them try a few of these on their own before proceeding.

Now let us reverse this relationship: Any six-digit number composed of two repeating sequences of three digits is divisible by 7, 11, and 13. For example,

We can also draw another conclusion from this interesting number 1,001. That is, a number with six repeating digits is always divisible by 3, 7, 11, and 13. Here is one such example. Have your students verify our conjecture by trying others.

What other relationships can be found that play on the symmetric nature of 1,001?

Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. These depend on the property described in above and the unusual property of the number 9.

Again, the number 9, which owes some of its unique properties to the fact that it is 1 less than the base 10, presents some nice peculiarities.

While playing with the number 9, you might ask your students to find an eight-digit number in which no digit is repeated and which when multiplied by 9 yields a nine-digit number in which no digit is repeated. Here are a few correct choices :

Here is another nice pattern to further motivate your students to search on their own for other patterns in mathematics. Again, not many words are needed to demonstrate the beauty of this pattern, for it is obvious at first sight.

Suprising Number Patterns III

Here are some more charmers of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Just look, enjoy, and spread these amazing properties to your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this. You might ask them why multiplying by 9 might give such unusual results. Once they see that 9 is one less than the base 10, they might get other ideas to develop multiplication patterns. A clue might be to have them consider multiplying by 11 (one greater than the base) to search for a pattern.

A similar process yields another interesting pattern. Might this give your students more impetus to search further?

Now the logical thing to inspect would be the pattern of these strange products.

How might you describe this pattern? Let students describe it in their own terms.

Panduan SEO dari Google

Google akhirnya merilis SEO starter guide atau panduan dasar SEO dalam 40 bahasa setelah sebelumnya hanya merilis dalam bahasa inggris.

link download dalam bahasa inggris
Search Engine Optimization Starter Guide
http://www.google.com/webmasters/docs/search-engine-optimization-starter-guide.pdf

link download dalam bahasa indonesia
Panduan Dasar SEO
http://www.google.co.id/intl/id/webmasters/docs/search-engine-optimization-starter-guide-id.pdf

Untuk yang gak mengerti bahasa inggris ataupun indonesia, silahkan melihat hlaman dibawah ini :
Google SEO Starter Guide
http://googlewebmastercentral.blogspot.com/2008/11/googles-seo-starter-guide.html

Kesimpulan.
Sayang sekali sepertinya format dalam bahasa indonesia ini hasil terjemahan kasar oleh Google Translator. Sehingga hasilnya kurang maksimal. Sampai-sampai lidah saya terlipat bacanya. hehehe. Anyway, saya bersyukur aja google udah SEO Starter Guide ini.

Suprising Number Patterns II

Here are some more charmers of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Just look, enjoy, and share these amazing properties with your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this.

In the following pattern chart, notice that the first and last digits of the products are the digits of the multiples of 9.

It is normal for students to want to find extensions of this surprising pattern. They might experiment by adding digits to the first multiplicand or by multiplying by other multiples of 9. In any case, experimentation ought to be encouraged.

Suprising Number Patterns I

There are times when the charm of mathematics lies in the surprising nature of its number system. There are not many words needed to demonstrate this charm. It is obvious from the patterns attained. Look, enjoy, and spread these amazing properties to your students. Let them appreciate the patterns and, if possible, try to look for an "explanation" for this. Most important is that the students can get an appreciation for the beauty in these number patterns.

Notice (below) how various products of 76,923 yield numbers in the same order but with a different starting point. Here the first digit of the product goes to the end of the number to form the next product. Otherwise, the order of the digits is intact.

Notice (below) how various products of 76,923 yield different numbers from those above, yet again, in the same order but with a different starting point. Again, the first digit of the product goes to the end of the number to form the next product. Otherwise, the order of the digits is intact.

Another peculiar number is 142,857. When it is multiplied by the numbers 2 through 8, the results are astonishing. Consider the following products and describe the peculiarity.

You can see symmetries in the products but notice also that the same digits are used in the product as in the first factor. Furthermore, consider the order of the digits. With the exception of the starting point, they are in the same sequence.

Now look at the product, 142,857 • 7 = 999,999. Surprised ?

It gets even stranger with the product, 142,857 • 8 = 1,142,856. If we remove the millions digit and add it to the units digit, the original number is formed.

It would be wise to allow the students to discover the patterns themselves. You can present a starting point or a hint at how they ought to start and then let them make the discoveries themselves. This will give them a sense of “ownership” in the discoveries. These are just a few numbers that yield strange products.

Menambahkan fitur menu develop pada safari windows dan mac

Safari adalah web browser dari Apple yang dikembangkan dari open source Webkit. Safari hingga tulisan ini dibuat telah mencapai versi 4. Dan browser safari ini tersedia di 2 OS yaitu Mac dan Windows.

Salah satu fitur yang mungkin jarang diketahui oleh para pengguna browser ini adalah adanya fitur menu “develop” yang berisi pilihan2 aneh (:P). Mungkin bagi sebagian orang menambahkan fitur ini akan memperlambat kinerja browser ini tapi bagi developer web, fitur ini menjadi sangat penting keberadaannya.

Oleh karena itu artikel kali ini akan membahas bagaimana cara menambahkan fitur menu develop pada safari agar dapat beroperasi seperti firebug pada firefox.

Untuk menampilkan fitur develop ini :

1. Pengguna Mac.

Apapun versi Safarinya, lewat command line, buka terminal window dan tulis perintah ini

defaults write com.apple.Safari WebKitDeveloperExtras -bool true
defaults write com.apple.Safari IncludeDebugMenu 1

2. Pengguna Windows

Untuk Safari 3.x
Masuk kedirektori dibawah ini sesuai OS anda :

Windows XP

C:\Documents and Settings\USERNAME\Application Data
\Apple Computer\Safari\Preferences.plist

Windows Vista

C:\Users\USERNAME\AppData\Roaming\Apple Computer
\Safari\Preferences.plist

Untuk Safari 4.x
Masuk kedirektori ini

C:\Program Files\Safari\Safari.resources\defaults.plist

Tambahkan perintah yang dicetak tebal pada file yang sesuai dengan versi Safari atau Windows anda.

<dict>
.....
<key>IncludeDebugMenu</key>
<true/>
</dict>

Restart Safari anda dan lihat hasilnya.

Cara singkat :

Heheh, tp saya punya cara yang singkat tanpa perlu restart Safari. Masuk Preferences Safari kamu, lalau pilih tab Advanced. Centangkan pilihan Show Develop menu in menu bar. Close window Preferences dan lihat hasilnya di menu bar akan sama hasilnya dengan cara2 susah diatas.

Membuat GWT Project pada IDE Eclipse

Google Web Toolkit (GWT) adalah framework open source yang dapat membantu kita dalam membuat Rich Internet Application (RIA) dengan menggunakan bahasa pemograman Java. Bagian terpenting dalam membuat RIA itu adalah Javascript, nah disini GWT akan membantu kita menerjemahkan kode Java kedalam Javascript. Tetapi bukan berarti dengan menggunakan GWT ini kita tidak diizinkan untuk membuat web dengan Javascript. Kita bahkan dapat memasukkan kode Javascript untuk berinteraksi dengan GWT. Bisa memasukkan jQuery, Dojo, dll.

Saya akan membagi tutorial ini menjadi 4 bagian

1. Menginstall GWT
2. Membuat Project GWT dengan utility scripts bawaan GWT
3. Import Project GWT ke IDE Eclipse
4. Menjalankan Project GWT

Menginstall GWT
Untuk menggunakan GWT ini, terlebih dahulu kita harus mendownload java2sdk dari sun. Untuk menginstall java2sdk ke windows atau linux silahkan lihat disini. Mendownload GWT dari http://code.google.com/webtoolkit. Saat tulisan ini dibuat GWT telah mencapai versi 1.6.4. Jika sudah mendownload GWT versi terbaru silahkan ekstrak ke direktori mana saja anda suka. Tetapi kali ini saya memilih di drive C:\

• gwt-servlet.jar dan gwt-user.jar adalah library yang mengandung GWT API. Kedua file ini dibutuhkan selama proses development dan runtime.

• gwt-dev-windows.jar adalah library yang spesifik bergantung pada OS yang dipakai. Librari ini mengandung GWT compiler dan file dll yang berhubungan pada saat mode Hosted. Untuk linux dan mac adalah gwt-dev-linux.jar dan gwt-dev-mac.jar.

• applicationCreator.cmd, benchmarkViewer.cmd, i18nCreator.cmd, junitCreator.cmd, dan projectCreator.cmd adalah comman line scripts atau batch yang akan membantu kita membuat aplikasi GWT. File-file ini selanjutnya saya sebut utility scripts.

• Direktori doc mengandung Javadoc untuk library GWT dan direktori samples mengandung contoh-contoh
  

Membuat Project GWT dengan utility scripts bawaan GWT
Saya tidak akan menjelaskan file-file didalam folder GWT lebih mendalam lagi karena sayapun masih pemula. Hehe. Ok. Kita langsung saja membuat aplikasi hello world sebagai awal. Disini saya akan membuat project GWT dengan nama myWeb yang berbasis IDE eclipse untuk IDE Netbeans liat disini. Gunakan projectCreator.cmd. masuk ke command prompt GWT ketikkan projectCreator.cmd -eclipse myWeb -out myWeb. Akan tampil :



Nah kemudian dengan applicationCreator.cmd.
Ketikkan applicationCreator.cmd -eclipse myWeb -out myWeb com.unhas. web.client.App. Akan tampil :



Import Project GWT ke IDE Eclipse
Klik kanan pada jendela project di Eclipse. Klik kanan ditempat yang kosong maksud saya.



Trus pilih import…, maka akan muncul jendela dibawah ini :



Pilih “Existing Projects into Workspace”. Kemudian klik tombol Next akan muncul jendela :



Klik tombol browse dan cari folder myWeb di folder ekstrak . Kemudian klik Finish. Dan project tadi akan di import ke IDE Eclipse kita yang hasilnya adalah sebagai berikut :


Umumnya pada setiap project GWT terdapat 2 buah folder yaitu client dan public. Seperti yang anda liat file dgn ekstensi .java selalu berada pada folder client dan file HTML ada pada folder public. Ini berarti kita dapat menambahkan file JSP, image, video, dll ke folder public.

Running GWT Project
Klik kanan pada file App.launch



Pilih Run As > App. Dan akan tampil 2 jendela sbb :



Inilah hasilnya dalam Hosted Mode. Jika ingin dalam Web Mode klik Compile/Browse:


Loh kok tampilannya bisa begitu, itu karena generated code yang dihasilkan dengan utility scripts pada bawaan GWT. Anda dapat merubahnya pada file App.java yang mengimplementasikan EntryPoint pada onLoadModule().

Cara menginstall Java SDK di Windows langkah demi langkah

Tutorial ini diperuntukkan bagi orang-orang yang amat sangat terlalu awam bagi dunia java (heheh…). Tutorial ini akan saya bagi menjadi 3 bagian, yaitu :

1. Menginstall Java SDK
2. Mengantur Environment Variables Windows
3. Mengcompile dan menjalankan program dengan Java

Menginstall Java SDK
Downloadlah terlebih dahulu Java SDK terbaru disini. Kali ini saya mempunyai Java SDK 6 Update 12.
Klik 2x program yang telah anda download tadi, sambil menunggu beberapa saat sampai muncul :



Kemudian kita akan dibawa ke window dibawah ini :



Klik tombol Accept dan kita akan dibawa ke window Custom Setup :



Terdapat 4 pilihan :

1. Development Tools, ini berisi tentang tools untuk membuat program java. Seperti compile, debug, dll.
2. Demos and Samples, ini berisi tentang demo dan sampel program dalam bahasa Java. Dan ini baik untuk dipelajari sorang pemula.
3. Source Code, ini berisi tentang source code java dari demo dan sampel.
4. Java DB, ini berisi tentang tools untuk berhubungan dengan engine database.

Kali ini saya akan menginstall semuanya kemudian klik tombol Next. Tunggu sampai proses menginstall selesai.





Klik tombol finish sebagai tanda proses instalasi telah selesai.

Coba pindah ke direktori C:\Program Files\Java, maka anda akan mendapatkan struktur direktori seperti dibawah ini :



Mengantur Environment Variables Windows
Selanjutnya kita akan mengatur lingkungan variabel windows. Pertama adalah lingkungan java runtime dan kedua adalah lingkungan JDK. Untuk memastikan apakah java runtime telah terinstal dengan baik, masuk ke sembarang direktori dengan cmd seperti dibawah ini :



Terlihat ada respon, ini berarti java runtime telah terinstall dengan baik. Bagaimana dengan JDKnya, masuk ke sembarang direktori dengan cmd seperti dibawah ini :



Terlihat bahwa javac sebagai compiler java tidak dikenali di lingkungan windows. Segera masuk ke System Properties Windows dengan mengklik-kanan icon My Computer lalu pilih Properties.





Pilih Environment Variables, Kemudian akan muncul jendela :



Pilih tombol New, bahwa kita akan membuat system variable baru. Liat alamat direktori jdk anda, lalu masukkan di Variable value seperti dibawah ini :


Pilih OK.

Pilih Edit.



Tambahkan %JAVA_HOME%\bin di Variable value. Ingat jangan menghapus nilai sebelumnya, kita Cuma menambahkan setelah karakter ;. Lalu pilih OK. Dan pilih OK lagi di jendela Environment Variables.


Untuk memastikan apakah settingan kita berjalan dengan baik. Buka jendela cmd yang baru, lalu ketikkan javac.



Ada respon. Berita baik, berarti settingan kita berjalan dengan baik.

Mengcompile dan menjalankan program dengan Java
Buat file baru dengan nama coba.java.
Lalu masukkan skrip dibawah ini :

public class coba{
public static void  main(String args[]){
System.out.println("oiiii  java ..... i'm coming");
}
}

Compile file coba.java dengan perintah javac coba.java. Jika ada error liat kembali skrip anda dan perintah compilenya. Berhasil tidaknya ditandai dengan tidak adanya respon dari compiler java.

Jalankan dengan coba.java dengan perintah java coba
Untuk lebih mudah silahkan lihat gambar dibawah ini :