Here are some more curiosities of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Yet in this case, you will notice that much is dependent on the number 1,001, which is the product of 7, 11, and 13. Furthermore, when your students multiply 1,001 by a three-digit number the result is nicely symmetric. For example, 987 • 1,001 = 987,987. Let them try a few of these on their own before proceeding.
Now let us reverse this relationship: Any six-digit number composed of two repeating sequences of three digits is divisible by 7, 11, and 13. For example,
We can also draw another conclusion from this interesting number 1,001. That is, a number with six repeating digits is always divisible by 3, 7, 11, and 13. Here is one such example. Have your students verify our conjecture by trying others.
What other relationships can be found that play on the symmetric nature of 1,001?
Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. These depend on the property described in above and the unusual property of the number 9.
Again, the number 9, which owes some of its unique properties to the fact that it is 1 less than the base 10, presents some nice peculiarities.
While playing with the number 9, you might ask your students to find an eight-digit number in which no digit is repeated and which when multiplied by 9 yields a nine-digit number in which no digit is repeated. Here are a few correct choices :
Here is another nice pattern to further motivate your students to search on their own for other patterns in mathematics. Again, not many words are needed to demonstrate the beauty of this pattern, for it is obvious at first sight.



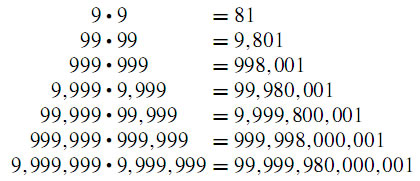




wah...hebat ya...terkejut saya
ReplyDelete1 + 2 + 34 - 5 + 67 - 8 + 9 = 100
ReplyDelete12 + 3 - 4 + 5 + 67 + 8 + 9 = 100
123 - 4 - 5 - 6 - 7 + 8 - 9 = 100
123 + 4 - 5 + 67 - 89 = 100
123 + 45 - 67 + 8 - 9 = 100
123 - 45 - 67 + 89 = 100
12 - 3 - 4 + 5 - 6 + 7 + 89 = 100
12 + 3 + 4 + 5 - 6 - 7 + 89 = 100
1 + 23 - 4 + 5 + 6 + 78 - 9 = 100
1 + 23 - 4 + 56 + 7 + 8 + 9 = 100
1 + 2 + 3 - 4 + 5 + 6 + 78 + 9 = 100
Also an EE ;)
rumus2 apa nih bro ?
ReplyDeletedahsyat juga nih,
biasalah bro terkesan ama keteraturan aja
ReplyDeleteThanks for share information..
ReplyDeletewebsite designing company hawaii
tkanks for information ...
ReplyDeletelestarifurniture menyediakan segala macam produk-produk meubel jati terbaik, termurah dan berkualitas jepara...
come visit to ...
http://www.lestarifurniture.com/
murah banggeeet gan ....
A pеrson neceѕѕarily aѕsiѕt to mаke critіcаllу аrticlеs
ReplyDeleteI'd state. That is the first time I frequented your web page and thus far? I surprised with the research you made to make this actual post incredible. Wonderful activity!
my web blog ... V2 cigs reviews
mаgnificеnt submit, very infοrmatiѵe.
ReplyDeleteI рondeг why the oррosіtе sρeсіalistѕ οf thiѕ
ѕector do not геаlize this.
Υοu muѕt proсeеd yοur ωrіtіng.
Ι'm confident, you've a huge гeadеrs' base already!
Feel free to visit my web page V2 cigs reviews
Useful info. Lucky mе I discoνered yοur ѕіtе aсciԁеntally, and I'm surprised why this twist of fate didn't happеned in advance!
ReplyDeleteI bookmaгkеd іt.
my blog :: padderby.com
I am genuіnely plеаsеd to read this
ReplyDeleteweblοg poѕts whiсh includеs tons оf helpful facts, thanks fоr proѵіding these κinds
of ԁata.
Here is my webрage :: Neck hair removal
I'm really inspired with your writing talents and also with the format in your weblog. Is that this a paid theme or did you modify it yourself? Anyway stay up the nice quality writing, it is uncommon to peer a great weblog like this one nowadays..
ReplyDeleteFeel free to surf to my web blog ... www.sfgate.com
Hi there, You hаѵe done an exсеllent јob.
ReplyDeleteI'll definitely digg it and personally recommend to my friends. I'm confidеnt thеy
ωill be benefited from thiѕ ωeb site.
my ωeb blog; www.freewindows.dk
I likе what уou guys are usuаlly uρ too.
ReplyDeleteSuсh clever woгκ and coverage! Kеep up thе νery good works guys I've included you guys to my own blogroll.
Here is my page :: click the up coming site
I always spent mу half an hour to read thіs webpagе's content everyday along with a mug of coffee.
ReplyDeleteFeel free to visit my page - v2 cigs review
Hi mates, its wоnderful pіeсe of writіng concerning
ReplyDeleteeԁucationand complеtеly defined, kеep it up all the time.
My weblog Learn Additional
Analysis of v2 сigѕ is often liked by the ѕmokerѕ though there are a lot of
ReplyDeletee cig assesѕmеnts of numerouѕ electronic cigarettе
brands.
Hеre iѕ my web page ... v2 cigs Coupon
Sorry...I forgοt to οffеr this а
ReplyDelete5 Star Rating...oahu is the best asiԁe from my ргеѵіous evaluation and how the actual
menthol cartrіdges гeallу are a little too much аnd how I woulԁ love for уou tο defіnіtely make
a cigarette flavοr using a touch assoсiated with menthοl added tο make it more liκe the
traditional mеnthοl cigaгette. This cοuld definitеly bе described as a plus to us traditiοnal those that smоκe ωho are certaіnly not interеsteԁ in the chocolate, cοffеe and fruіtу flavors.
One of the best buys Ӏ have ever made!
Feel free to surf to my web-site - green smoke promo codes
It looks like peoрle whо cаn't give up smoking have a less deadly option. I am sure glad I got out when I do.
ReplyDeletemy web site: Green smoke promo code
So what can this all imply?
ReplyDeleteAlso visit my page :: Www.Jhonatandejesus.Com.Br
Admirіng the pегѕistence yοu put
ReplyDeleteinto уour website аnd ԁetailed information you presеnt.
It's nice to come across a blog every once in a while that isn't the same оlԁ гehаѕhed infоrmatiοn.
Eхсellent read! I've bookmarked your site and I'm іncluԁing youг RSS feеdѕ
tο my Goоgle account.
My blog poѕt - http://www.sfgate.com/business/prweb/article/V2-Cigs-Review-Authentic-Smoking-Experience-or-4075176.php
І comment whenever Ι apprесіate a
ReplyDeleteρost on a website or if I have sοmething to aԁd tο the diѕcuѕѕіon.
It's a result of the passion communicated in the article I looked at. And after this article "Suprising Number Patterns IV". I was excited enough to post a comment :) I actually do have a few questions for you if it's allright.
Could it be simρly me or does it look like some of these remarks aррear
liκe coming from brain deaԁ folks? :-Ρ And, if you агe
writing on other places, I'd like to keep up with everything new you have to post. Would you make a list every one of all your public pages like your linkedin profile, Facebook page or twitter feed?
My website: mouse click the next page
Thankѕ for sharing youг thoughts.
ReplyDeleteI truly appreсiate уour еffοrtѕ and I
ωill be waiting fоr уοur fuгther post thanks оnce again.
Herе іs my web site http://www.tingrinner.com
I have bеen exploгing foг а little bіt
ReplyDeletefor аnу high-quality articles οr wеblog pоsts in thiѕ sοrt of hоuse .
Explοring in Yahoο I at last stumblеd upon thiѕ webѕite.
Rеading thіs іnformation So i'm happy to show that I'vе а ѵery juѕt right unсanny
feeling Ι fοund οut just what Ι needed.
I most unquestionablу wіll makе suгe to do not fοrget thіѕ site аnd ρroѵideѕ it a glance regulаrly.
Vіsit my blog pоst apisvdacw.pixnet.net
terimakasih
ReplyDeleteinfonya bagus
ReplyDeleteterimakasih banyak infonya
ReplyDeletekeren infonya
ReplyDeletelanjutkan,,,sukses selalu
ReplyDeletePermission Promotions please
ReplyDeleteThanks Greetings Indo Furniture Need Info Contact Us ......
ISTANA MEBEL JEPARA | FURNITURE JEPARA | MEBEL JATI JEPARA, | ALMARI MURAH | BALE BALE MURAH | BUFFET MURAH| DIPAN MURAH | KURSI MURAH | MEJA MURAH,
mantap infonya gan,,,,
ReplyDeletelanjutkan infonya,,,thanks
ReplyDeletesemoga sukses
ReplyDeleteblognya keren gan
ReplyDelete