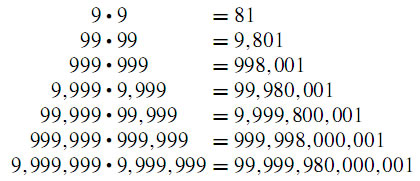Here are some more curiosities of mathematics that depend on the surprising nature of its number system. Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. Yet in this case, you will notice that much is dependent on the number 1,001, which is the product of 7, 11, and 13. Furthermore, when your students multiply 1,001 by a three-digit number the result is nicely symmetric. For example, 987 • 1,001 = 987,987. Let them try a few of these on their own before proceeding.
Now let us reverse this relationship: Any six-digit number composed of two repeating sequences of three digits is divisible by 7, 11, and 13. For example,
We can also draw another conclusion from this interesting number 1,001. That is, a number with six repeating digits is always divisible by 3, 7, 11, and 13. Here is one such example. Have your students verify our conjecture by trying others.
What other relationships can be found that play on the symmetric nature of 1,001?
Again, not many words are needed to demonstrate the charm, for it is obvious at first sight. These depend on the property described in above and the unusual property of the number 9.
Again, the number 9, which owes some of its unique properties to the fact that it is 1 less than the base 10, presents some nice peculiarities.
While playing with the number 9, you might ask your students to find an eight-digit number in which no digit is repeated and which when multiplied by 9 yields a nine-digit number in which no digit is repeated. Here are a few correct choices :
Here is another nice pattern to further motivate your students to search on their own for other patterns in mathematics. Again, not many words are needed to demonstrate the beauty of this pattern, for it is obvious at first sight.